Aptitude Height And DistancePage 1
1. |
|
Answer is: B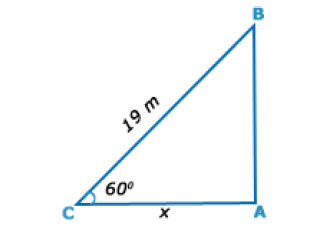
Let AB be the wall and BC be the ladder.
Then, < ABC = 60°
and, BC = 19 m.;
AC = x metres
AC/BC = cos 60°
x / 19 = 1 / 2
x = 19/2
x = 9.5 m.

Let AB be the wall and BC be the ladder.
Then, < ABC = 60°
and, BC = 19 m.;
AC = x metres
AC/BC = cos 60°
x / 19 = 1 / 2
x = 19/2
x = 9.5 m.
2. |
|
Answer is: DLet AB be the wall and BC be the ladder.

Then, < ABC = 60°
AC = 4.6 m.;
AC/BC = cos 60° = 1 /2
BC = 2×AC
BC = (2× 4.6) m
BC = 9.2 m

Then, < ABC = 60°
AC = 4.6 m.;
AC/BC = cos 60° = 1 /2
BC = 2×AC
BC = (2× 4.6) m
BC = 9.2 m
3. |
|
Answer is: ALet AB be the tree and AC be its shadow.
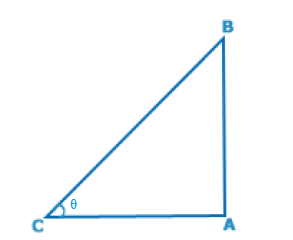
Then, < ABC = θ.
then, AC/AB = √3
Cot θ = √3 = cot 30°
θ = 30°

Then, < ABC = θ.
then, AC/AB = √3
Cot θ = √3 = cot 30°
θ = 30°
4. |
|
Answer is: CLet AB be the pole and AC be its shadow.
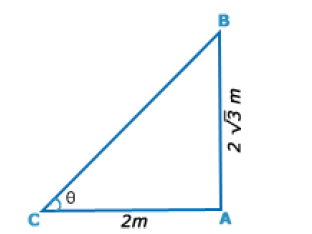
Then, < ACB = θ.
Then, AB= 2 √3 m, AC = 2m,
Tanθ = AB/AC = 2√3/2 = √3
θ = 60°

Then, < ACB = θ.
Then, AB= 2 √3 m, AC = 2m,
Tanθ = AB/AC = 2√3/2 = √3
θ = 60°
5. |
|
Answer is: DOne of AB, AD and CD must have been given.So, the data is inadequate.
6. |
|
Answer is: B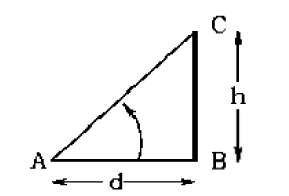
Let BC represent the tower with height h = 30 m, and A represent the point where the man is standing. AB = d denotes the distance of the man from
tower.
The angle subtended by the tower is A = 60o
From trigonometry,
tan A = tan 60o = h / d = √3
So d = 30/√3 s m
Hence the distance of the man from the tower is 17.32 m

Let BC represent the tower with height h = 30 m, and A represent the point where the man is standing. AB = d denotes the distance of the man from
tower.
The angle subtended by the tower is A = 60o
From trigonometry,
tan A = tan 60o = h / d = √3
So d = 30/√3 s m
Hence the distance of the man from the tower is 17.32 m
7. |
|
Answer is: A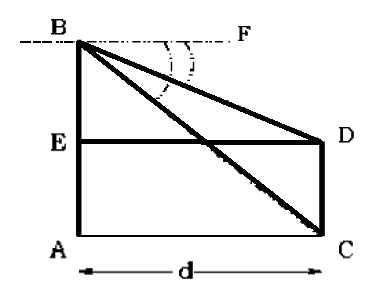
The first tower AB and the second tower CD are depicted in the figure on the left.
First consider the triangle BAC. Angle C = 60o
tan BCA = tan 60o = AB/AC
This gives AB = d tan 60o
Similarly for the triangle BED, BE = d tan 30o
Now height of the second tower CD = AB − BE = d (tan 60o − tan 30o)
CD = 25 (√3 − 1/√3) = 25 × 2/√3 = 28.87 m.

The first tower AB and the second tower CD are depicted in the figure on the left.
First consider the triangle BAC. Angle C = 60o
tan BCA = tan 60o = AB/AC
This gives AB = d tan 60o
Similarly for the triangle BED, BE = d tan 30o
Now height of the second tower CD = AB − BE = d (tan 60o − tan 30o)
CD = 25 (√3 − 1/√3) = 25 × 2/√3 = 28.87 m.
8. |
|
Answer is: B
The situation is depicted in the figure with CD representing the tower and AB being the distance between the two men.
For triangle ACD,
tan A = tan 60o = CD / AD
Similarly for triangle BCD,
tan B = tan 45o = CD/DB
The distance between the two men is
AB = AD + DB = (CD/tan 60o) + (CD/tan 45o)
AB = (26/√3) + (26/1) = 41.01 m

The situation is depicted in the figure with CD representing the tower and AB being the distance between the two men.
For triangle ACD,
tan A = tan 60o = CD / AD
Similarly for triangle BCD,
tan B = tan 45o = CD/DB
The distance between the two men is
AB = AD + DB = (CD/tan 60o) + (CD/tan 45o)
AB = (26/√3) + (26/1) = 41.01 m
Comments
No comment yet.