Aptitude Height And DistancePage 2
9. |
|
Answer is: A
In the figure, A and B represent the two men and CD the tall building.
tan A = tan 30o = DC/AC = h/AC; and
tan B = tan 60o = DC/BC = h/BC
Now the distance between the men is
AB = x = AC − BC = (h/tan 30o) − (h/tan 60o)
AB = (120√3 ) − (120/√3 ) = 138.56 m.

In the figure, A and B represent the two men and CD the tall building.
tan A = tan 30o = DC/AC = h/AC; and
tan B = tan 60o = DC/BC = h/BC
Now the distance between the men is
AB = x = AC − BC = (h/tan 30o) − (h/tan 60o)
AB = (120√3 ) − (120/√3 ) = 138.56 m.
10. |
|
Answer is: B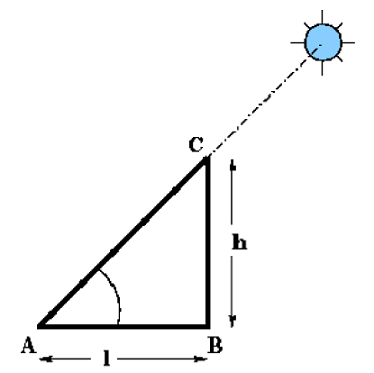
In the figure, BC represents the pole and AB its shadow.
tan A = BC / AB = h / l = 50 / 50.00 = 1.000
From trigonometric tables, we note that
tan A = 1.000 for A =45o
Hence the angle of elevation of the sun at this point of time is 45o

In the figure, BC represents the pole and AB its shadow.
tan A = BC / AB = h / l = 50 / 50.00 = 1.000
From trigonometric tables, we note that
tan A = 1.000 for A =45o
Hence the angle of elevation of the sun at this point of time is 45o
11. |
|
Answer is: C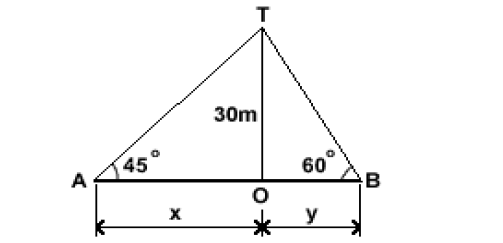
Let OT be the tower.
Therefore, Height of tower = OT = 30 m
Let A and B be the two points on the level ground on the opposite side of tower OT Then, angle of elevation from A = TAO = 45o and angle of elevation from B = TBO = 60o
Distance between AB = AO + OB = x + y (say)
Now, in right triangle ATO,
tan 45o = OT/AT = 30/x
x = 30/tan45o = 30 m
And in right triangle BTO,
tan 60o = OT/OB = 30/y
y = 30/tan60o = 30/√3 = 30√3/3 = 17.32 m
Hence, the required distance = x + y = 30 + 17.32 = 47.32 m

Let OT be the tower.
Therefore, Height of tower = OT = 30 m
Let A and B be the two points on the level ground on the opposite side of tower OT Then, angle of elevation from A = TAO = 45o and angle of elevation from B = TBO = 60o
Distance between AB = AO + OB = x + y (say)
Now, in right triangle ATO,
tan 45o = OT/AT = 30/x
x = 30/tan45o = 30 m
And in right triangle BTO,
tan 60o = OT/OB = 30/y
y = 30/tan60o = 30/√3 = 30√3/3 = 17.32 m
Hence, the required distance = x + y = 30 + 17.32 = 47.32 m
12. |
|
Answer is: B
In Triangle ABC,
Sin 30 = AB/AC
1/2 = AB/20
AB = 10 m

In Triangle ABC,
Sin 30 = AB/AC
1/2 = AB/20
AB = 10 m
13. |
|
Answer is: Blet us use the previous figure

Here, BC = 8 m
or, tan 30 = AB/BC
Or, 1/√3 = AB/8
Or, AB = 8/√3 = 4.61 m
Now, cos 30 = √3/2 = BC/AC = 8/AC
Or, AC = 16/√3
Height of tree = AB + BC = 8/√3 + 16/√3 = 24/√3 = 8√3

Here, BC = 8 m
or, tan 30 = AB/BC
Or, 1/√3 = AB/8
Or, AB = 8/√3 = 4.61 m
Now, cos 30 = √3/2 = BC/AC = 8/AC
Or, AC = 16/√3
Height of tree = AB + BC = 8/√3 + 16/√3 = 24/√3 = 8√3
14. |
|
Answer is: C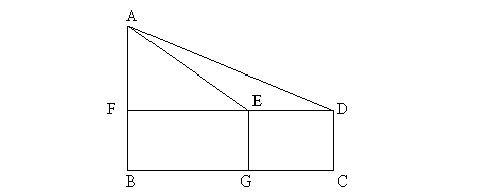
Given that, AB = 30 m(Height of building)
DC = EG = 1.5 m(Height of building)
Angle D = 30o
Angle E = 60o
AF = 30 - 1.5 = 28.5 m
In Triangle AFD, tan30o = AF/FD = 28.5/FD
Or, 1/√3 = 28.5/FD
Or, FD = 28.5/√3
In Triangle AFE, tan60o = AF/FE = 28.5/FE
Or, √3 = 28.5/FE
Or, FE = 28.5/√3
Required distance = ED = 28.5√3 - 28.5/√3
ED = 28.5√3 - 9.5√3 = 19√3

Given that, AB = 30 m(Height of building)
DC = EG = 1.5 m(Height of building)
Angle D = 30o
Angle E = 60o
AF = 30 - 1.5 = 28.5 m
In Triangle AFD, tan30o = AF/FD = 28.5/FD
Or, 1/√3 = 28.5/FD
Or, FD = 28.5/√3
In Triangle AFE, tan60o = AF/FE = 28.5/FE
Or, √3 = 28.5/FE
Or, FE = 28.5/√3
Required distance = ED = 28.5√3 - 28.5/√3
ED = 28.5√3 - 9.5√3 = 19√3
15. |
|
Answer is: B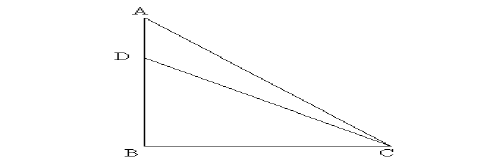
Height of building = DB = 20 m
Angle DCB = 45o
Angle ACB = 60o
In Triangle DBC, tan45o = 1 = DB/BC
Or, Db = BC = 20 m
In Triangle ABC, tan60o = √3 = AB/BC
Or, AB = 20√3
Now, AD = AB - DB = 20√3 - 20
AD = 20(√3 - 1) = 20(1.732 - 1)
AD = 20 x 0.732 = 14.64 m

Height of building = DB = 20 m
Angle DCB = 45o
Angle ACB = 60o
In Triangle DBC, tan45o = 1 = DB/BC
Or, Db = BC = 20 m
In Triangle ABC, tan60o = √3 = AB/BC
Or, AB = 20√3
Now, AD = AB - DB = 20√3 - 20
AD = 20(√3 - 1) = 20(1.732 - 1)
AD = 20 x 0.732 = 14.64 m
16. |
|
Answer is: A
Height of tower = AB = 50 m
Angle ACB = 60o
Angle DBC = 30o
In Triangle ABC, tan60o = √3 = 50/BC
Or, BC = 50/√3
In Triangle, DCB, tan30o = 1/√3 = DC/BC
Or, DC = 50/3

Height of tower = AB = 50 m
Angle ACB = 60o
Angle DBC = 30o
In Triangle ABC, tan60o = √3 = 50/BC
Or, BC = 50/√3
In Triangle, DCB, tan30o = 1/√3 = DC/BC
Or, DC = 50/3
Comments
No comment yet.